5) Sound Power Level

For the quantification of the noise intensity, and in order to compare one cooling fan configuration with another, it is at least necessary to have a relationship between the noise intensity and important design parameters like pressure drop, flow, fan speed, and fan diameter. Through years of research and field measurements Hudson has developed the following relationship;

Sound Power Level (PWL) = C + 30 Log(Tip Speed/1000) + 10 Log(hp) - 5 Log (Dia.) + f

The characteristic value C represents the influence of the fan shape on the noise generating phenomena or as practically said before, the intensity and quantity of swirls. From formula above it becomes clear that especially the tip speed has a strong influence factor on the sound power level. The correction term f is related to characteristic noise mechanisms which have been referred to already; the influence of obstructions like fan supports, the influence of the flow inlet shape, pitch angle, and tip clearance, etc. The influence of obstructions both on inlet and outlet is defined as a function of the swept area of the obstruction and the area of the fan section.

6) PWL per Octave Bands

The sound spectrum (linear) can be obtained by adding the correction factors stated below to PWL dB(A). The correction is independent of blade passing frequency.

In case of PWL = 104.8 dB(A), the PWL per octave bands are as follows:

7) Sound Pressure Level (SPL)

Acceptable noise levels are generally specified as a sound pressure level expressed in decibels (linear) or A-rated decibels (dB(A)), that may not be exceeded when measured at a certain distance from the noise generating equipment. The specified distance may be by the plant boundary or a given noise sensitive location, such as a residential area.

This SPL is a noise at a point from the sound source. It is the sound we measure, while the sound power level can not be measured directly. Measurements for community noise requirements are made at the plant boundary or nearest residence in the far field of the cooling tower. The far field is defined as the region where there is a linear relationship between the sound pressure level measured and the distance from the noise source.

In the far field, the sound pressure level will drop 6 dB with each doubling of distance. The far field will generally begin at a distance of four times the largest machine dimension. For instance, if a cooling tower is 20 ft x 30 ft, then the far field will begin at 120 ft from the source. In the far field, the sound pressure level can be calculated by

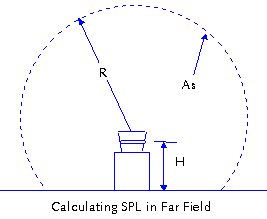
SPL = PWL - 10 Log (As) + 0.23 (As in ft² is the surface area over which noise is radiated.)

Noise will tend to radiate from a non-directional source uniformly in all directions. Sound pressure waves move spherically away from the source. The radius of this sphere is the distance to the measurement point. However, if there is a reflective surface impeding spherical radiation, then the radiation will become only partially spherical. In this case, the surface area also depends on the height of the noise source above the ground. In this case, As = 2pR(R + H). If the height goes to zero, the radiation takes on a hemispherical shape and As = 2pR².

In plant noise requirements are generally in the near field of the noise source. In this region, sound pressure levels are difficult to predict because of the non-linear relationship between sound pressure level and distance from the source. Also, noise sources that are not directional in the far field may be directional in the near field.

The calculation procedure specified below can be used in case there is a fan stack with a minimum height of 0.35 x fan diameter and a maximum of 1 x fan diameter.

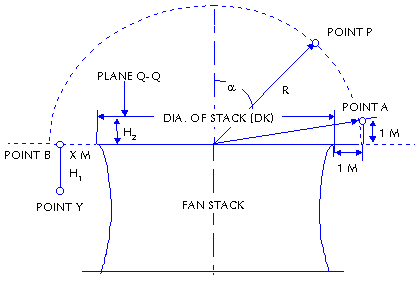
(1) Sound Pressure Level in Point P = PWL - 2 - 10 Log 2pR² + ( - 6.8 (1-(Cos a)^0.5))
(Note that this equation could be applied to a case that the radius R is within the distance of 5 times the diameter of fan stack top and a is smaller than 90 deg.

(2) Sound Pressure Level in Point A = PWL - 2 - 10 Log 2pR² + (2 - 6.8 (1 - (1/R)^0.5))

(3) Sound Pressure Level in Point B = PWL - 2 - 10 Log 2pDK² - 4.8 + 4 (1 - R/DK)

(4) Sound Pressure Level in Point Y = SPL in Point B - 1.5

(5) Sound Pressure Level in Plane Q - Q = PWL - 2 - Log pDK(DK/4 + H)

Let's calculate the sound pressure levels for the example of PWL of one fan is 101 dB(A) and the diameter of fan stack top is 10.119 m.

(1) SPL at Point P: R = 50 meters, a = 87.8,
then SPL = 101 - 2 - 10 Log (2 x 3.1416 x 50²) + (2 - 6.8 x (1 - Cos 87.8^0.5) = 53.57 dB(A)

(2) SPL at Point A: R = [(10.119/2 + 1)² + 1]^0.5 = 6.14146 M
then SPL = 101 - 2 - 10 Log (2 x 3.1416 x 6.14146²) + (2 - 6.8 x (1 - (1/6.14146)^0.5) = 73.20 dB(A)

(3) SPL at Point B: R = (10.119/2) + 1.025 = 6.08 M
then SPL = 101 - 2 - 10 Log (2 x 3.1416 x 10.119²) + (2 - 6.8) + 4 x (1 - 6.08/10.119) = 67.71 dB(A)

(4) SPL at Point Y: R = 6.08 M, H₁ = 0.5 M
then SPL = SPL at Point B - 1.5 = 66.21 dB(A)

(5) SPL at Plane Q - Q: H₂ = 1 M
then SPL = 101 - 2 - 10 Log [3.1416 x 10.119 x (10.119/4 + 1)] = 78.50 dB(A)

(6) SPL at Point of Residence: This is required to analysis the noise specially.

8) Noise Calculation from Two or More Noise Sources

From two or more difference noise levels, the total sound pressure level can be calculated per the formula of 10 Log (10 ^{0.1 x SPL1} + 10 ^{0.1 x SPL2} ... + 10 ^{0.2 x SPLn-1} + 10 ^{0.1 x SPLn}). This is very useful to obtain the resultant of different SPL at a point. For example, if the background noise level at a point is 53 dB(A) and the noise level due to a mechanical equipment is 59 dB(A), the total noise level at a given point is obtained from 10 x Log (10 ^{0.1 x 53} + 10 ^{0.1 x 59}) and the result is 59.97 dB(A).

Also, the noise subtraction from a noise level can be obtained from a formula of 10 Log (10 ^{0.1 x SPL1} - 10 ^{0.1 x SPL2}). This is frequently used to guess a noise due to mechanical equipment from a measurement of noise at a point. For example, when the noise level at a point is 55 dB(A) and the background noise at that point is 53 dB(A), let's calculate a noise level due to the mechanical equipment.

SPL = 10 x Log (10 ^{0.1 x 5.5} - 10 ^{0.1 x 5.3)} = 50.67 dB(A).

9) Reduction of Fan Noise

Design is the primary factor affecting the fan noise. The blade design determines the pressure capability of the blade. Since the pressure is proportional to the fan speed squared, added pressure capability means a fan can run slower and do the same work. From above equation representing the sound power level from a fan, it is clear that an approach for achieving the noise reduction is to look as decreasing the characteristic value C and/or the tip speed of fan without reducing the pressure drop, flow, or fan efficiency.

Reduction of the tip speed of a fan will indeed reduce the noise generated, however it will also reduce the pressure and flow. The reduction of pressure and flow can be avoided by making the blades wider. Wider blades perform aerodynamically the same as narrow ones, but at lower speed. This is similar to a sail-plane which can fly at a lower speed than a motorized plane because of its bigger wing area. The relative width of the fan blades is expressed by the total width of the fan blades to the fan circumference in the so called solidity number.

It is evident that it is possible to make a significant improvement by making the fan blades wider. The reduction of noise generation can be almost totally yet simply explained by the possibility of reducing the tip speed, which decreases the quantity and intensity of swirls. This is attributed with a shifting to the lower frequencies, which is favorable for the A-weighted noise spectrum.

The application of low noise fans has an enormous impact on the costs of construction and performance of cooling towers. The consequences can be considered from two principle positions.

• Avoiding of the application of sound attenuators: Sound attenuators are expensive as well as power and space consuming.
• Higher loading and performance of an existing cooling tower: If a certain PWL value is acceptable for a particular application, then it is possible to operate the existing tower with a low noise fan with a much bigger flow than with a standard fan.