6) Breakpoint Phenomenon

The chemistry of this phenomenon is based on the inorganic reaction of chlorine with ammonia nitrogen. In dilute aqueous solution (1 - 50 mg/l) the reaction between ammonia nitrogen and chlorine forms three types of chloramines in the following reactions:

HOCl + NH₃ ---> NH₂Cl (monochloramine) + H₂O ------ Eq. 1
NH₂Cl + NH₃ ---> NHCl₂ (dichloramine) + H₂O ------ Eq. 2
NHCl₂ + HOCl ---> NCl₃ (trichloramiine) + H₂O ------ Eq. 3

These reactions are in general by steps, so that they all complete with each other. A series of complex reactions with all of these substances involves the chlorine substitution of each of the hydrogen atoms in the ammonia molecule. These competing reactions are grossly dependent upon pH, temperature, contact time, initial chlorine to ammonia ratio, and most of all upon the initial concentrations of chlorine and ammonia nitrogen. Note that in all three equations the chlorine atom is positively charged.

Above Eq. 1 will convert all of the free chlorine to mono chloramine at pH 7 to 8 when the ratio of chlorine to ammonia is equimolar (5:1 by weight) or less - that is, 4:1, 3:1, and so on. The rate of this reaction is extremely important, since it is pH-sensitive. According to reaction rates established by Morris, the fastest conversion of HOCl to NH₂CL occurs at pH 8.3. The following are calculated reaction rates for 99 percent conversion of free chlorine to monochloramine at 25^oC with a molar ratio of 0.2 x 10-3 mol/l HOCl and 1.0 x 10-3 mol/l NH₃:

The reaction slows appreciably as the temperature drops. At 0^oC, it requires nearly five minutes for 90 percent conversion at pH 7. The pH dependence of this reaction is described accurately on the basis of the HOCl^- OCl^- equilibrium and the NH₃- NH₄ + equilibrium.

The reaction of Eq. 2 will form dichloramine between pH and 8 if the ratio of chlorine to ammonia is 2 mol chlorine to one mol ammonia nitrogen (10:1 by weight). The rate of this reaction is much slower than that of equation 1. It may take as long as one hour for 90 percent conversion and up to five hours at pH 8.5 and above when ammonia nitrogen concentrations are very low. As the pH approaches 5 the reaction speeds up appreciably. This reaction is dependent upon pH, initial ammonia nitrogen, and temperature. The reaction time of Eq. 2 is known to be minute when the initial nitrogen concentration is in excess of 1 mg/l and pH is favorable.

The reaction of Eq. 3 will form some trichloramine (commonly called nitrogen trichloride when the pH is between 7 and 8 if the chlorine to ammonia nitrogen ratio is 3 mol of chlorine to 1 mol of ammonia nitrogen (15:1 by weight). At present very little is known about the kinetics of this reaction, particularly in concentrations of less than 10 ppm (10-4 M). Nitrogen trichloride does form, even at equimolar ratios of chlorine to ammonia nitrogen, if the pH 5, if the pH is depressed to 5 or less. At one time it was thought that it would not form above pH 5. It is known to exist in water treatment plants when the pH is as high as 9. This occurs at very high chlorine to ammonia nitrogen ratios (25:1 by weight).

In cooling water practice, if the chemistry of Eq. 1 is practiced, it is known as either the chlorine-ammonia process, the chloramine process or chloramination. Eq. 2 and 3 are related to the "breakpoint" phenomenon. It was Griffin's work which let to the discovery of this phenomenon in 1939. Grffin was attempting to explain the sudden loss of chlorine residuals and the simultaneous disappearance of ammonia nitrogen at treatment plants which were experimenting with higher than usual chlorine residuals (2 - 15 mg/l).

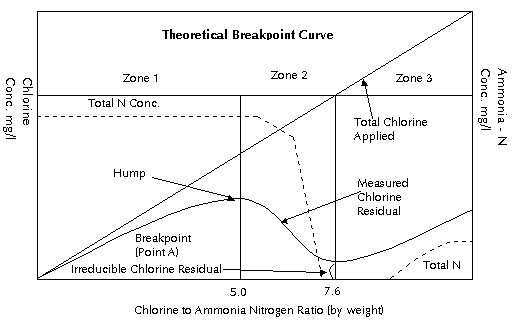
The breakpoint curve below is a graphic representation of chemical relationships which exist as varying amounts of chlorine are added to waters containing small amount of ammonia nitrogen. The theoretical breakpoint curve is shown in below. It was originally developed as a result of Griffin's work. This curve has several characteristic features. The principal reaction in Zone 1 is the reaction between chlorine and the ammonia ion indicated in Eq. 1. This results in a chlorine residual containing only monochloramine all the way to the hump in the curve. The hump occurs, theoretically, at a chlorine to ammonia nitrogen weight ratio of 5:1 (molar ratio 1:1). This ratio indicates the point where the reacting chlorine and ammonia nitrogen molecules are present in solution in equal numbers. As the molar ratio begins to exceed 1:1, some of the monochloramine starts a disproportionation reaction to form dichloramine in accordance with Eq. 2.

To the right of the breakpoint, Zone 3, chemical equilibria require the buildup of free chlorine residual (HOCl). In practical applications of breakpoint chlorination, reactions occur which result in the formation of nitrogen gas, nitrate, nitrogen trichloride, and other end products. These reactions consume chlorine and cause the Cl₂:NH₄ + ratio to exceed the stoichiometric value of 7.6:1 and affect the shape of the breakpoint curve.

As the chlorine to ammonia nitrogen ratio increases beyond about 12 - 15:1 the reaction of equation 3 sets in. Under these conditions the formation of nitrogen trochloride will occurs even at pH values as high as 9. As the chlorine dose is increased beyond point A in Zone 3, the free available chlorine residual will increase in an amount equal to the increase in the dosage. Therefore, the breakpoint curve in Zone 3 should plot at a 45^o angle.

It should be emphasized that the shape of the breakpoint curve is affected by contact time, temperature, concentration of chlorine and ammonia, and pH. High concentrations increase the speed of the reactions. As the pH decreases below 8.3, the reactions are retarded. The higher the temperature, the faster the reactions. The shape of the curve is different for different contact times.

In water practice this is known as free residual chlorination rather than the breakpoint process. In water treatment the practical significance of the curve is briefly as follows:

• Zone 1: The residual in this zone up to the hump are all monochloramine. The residuals in this zone do not form trichloramines.
• Zone 2: As the hump is passed, the monochloramine plus the addition of more free chlorine begins to form dichloramine, which is about twice as germicidal as monochloramine. However, this may not be the best part of the curve for the production of a palatable water.
• Zone 3: At the tip of the curve (point A) and beyond, free chlorine residual will appear. The total residual will be made up of the nuisance residuals plus free chlorine. If nitrogen trichloride is formed, it will appear in this zone. In practice it has been found that a ratio of free chlorine to total residual of 85 percent or greater will result in the most palatable water.

   

7) Alkalinity

Since chlorine solutions are highly corrosive the application of chlorine to a process stream will often raise the question of chlorine corrosion. Corrosion by chlorine is related directly to pH, which is dependent upon alkalinity. Therefore it is appropriate to know the effect of chlorine on the alkalinity of a water.

If a water is dosed with chlorine to the extent of the chlorine demand of the water, all of the chlorine applied will end up as chloride ion (Cl^-) as follows:

Cl₂ + H₂O ---> HOCl + HCl ------ Eq. 4
HOCl + Cl demand + HCl ---> 2HCl ------ Eq. 5

This calculate as 1.4 parts alkalinity for each part chlorine:

2 HCl + H₂O + CaCO₃ ---> CaCl₂ + CO₂ + 2 H₂O ------ Eq. 6
Alkalinity as CaCO₃ = 100 / Cl₂ = 100 / 71 = 1.4

The reaction in Eq. 6 occurs at pH 4.3, which is the endpoint of the alkalinity titraion, and where CO₂ exists. When HOCl is not reduced, only one Cl goes to HCl and the reaction consumes just half of the alkalinity, or 0.7. As can be seen from the above, the subject of alkalinity destruction by chlorine is not a simple one.

Take the case where water has sufficient alkalinity to maintain a 7.0 pH, and none of the chlorine applied is consumed by chlorine demand. In this case 50 percent of the chlorine applied will go to HCl. Eighty percent of the remaining 50 percent will be undissociated HOCl and unreactive in the alkalinity reactions. However, the other 20 percent of the remaining 50 percent at pH 7 is H⁺ and OCl^-.

The alkalinity reduction is calculated as follows:

50% + (0.20 x 50%) = 60%

0.6 x 1.4 = 0.84 parts alkalinity reduction by chlorine at pH 7.0. The rule of thumb for alkalinity correction by the use of caustic to maintain pH is a pound of caustic to a pound of chlorine. One part of caustic produces 1.25 parts of alkalinity. If a water at pH 7 is dosed with chlorine, and the demand is 6 mg/l, then the alkalinity reduction is 1.3 parts of alkalinity for each part of chlorine. This rule is reliable.