(3) Guillotine Break in a Pipeline

Ton Container Supply:
The maximum size of a chlorine header system under pressure in any applications should never be larger than one inch. If the installation involves liquid withdrawal from ton containers, then evaporators will be an integral part of the chlorine supply system. Therefore, the worst-case scenario would be a rupture in the liquid header between the containers and the evaporators. To simplify the concept let the calculations be confined to one container, one evaporator, and 100 ft length of one-inch header pipe in the length.

The liquid exiting the container must pass through a 3/8 inch tubing in the dished head -then through the container shutoff valve, then through the auxiliary container shutoff valve, and finally through the header valve. All of these components are flow restrictors compared to a one-inch pipe. So how can these restrictions be accounted for in calculating the chlorine leak rate?

Circa 1950, the operating personnel needed to know the maximum possible liquid withdrawal rate from a single ton container, at the East Bay Municipal Utility District wastewater treatment plant, Oakland, California. Their Chlorinator capacity was 18,000 lb/day. Their test, which they performed several times, indicated that the maximum rate was only about 10,200 lb/day. The pressure drop between the container and the entrance to the chlorinator was on the average about 85-40 psi = 45 psi because there was a pressure- reducing valve between the evaporator and the chlorinator. The flow at this pressure drop has to be recalculated to reflect a zero pressure at the leak. To apply a worst-case situation, let us assume a container pressure of 120 psi.

Using the Chlorine Institute formula:

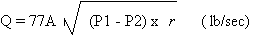
Where:
Q = 10,200 lb/day = 0.1181 lb/sec
r = 88 lb/ft³

Substituting this in the above formula, the value of the unknown, 77A, can be found:

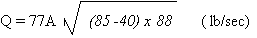
Q = 0.1181 lb/sec = 77A x 62.93
77A = 0.00188

Assuming a cylinder pressure of 120 psi, chlorine density at 88 lb/ft and substituting 77A = 0.00188 in above equation, the leak rate Q will be:

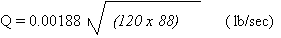
Q = 0.1899 lb/sec x 60 = 11.4 lb/min

This then is the worst-case leak rate from a single ton container "on-line", when there is a guillotine break in the liquid chlorine header piping. It is obvious that if ton containers are being used for liquid withdrawal, an evaporator is part of the system. Therefore, when there is a guillotine break in the liquid header, the contents of the evaporator becomes part of the leak.

Powell found by actual test that the maximum liquid withdrawal from an inverted 150-lb cylinder was 20 lb/min at 90 psi cylinder pressure. The restrictions in this instance were the cylinder valve and 3-4ft of 3/8 inch tubing.

All chlorine evaporators are designed to vaporize at a temperature variation between 160 and 180^oF, regardless of the chlorine feed rate. This means that the level of liquid chlorine in the evaporator remains fairly constant. It is safe to conclude that the evaporator content is never more than 100 lb. At 20 lb/min., the evaporator will empty in about 5 minutes because of the chlorine header rupture. Therefore, the probable maximum chlorine release rate will be 11.4 + 20 lb/min. for the first 5 minutes and then 11.4 lb/min after that interval. This is for each ton container "on line" and each evaporator.

Such a leak will cool the room so quickly that vaporization is temporarily stopped. During this time, if the container floor area has been designed properly, the liquid chlorine will flow through the collecting slots in the floor and be hustled off to the scrubber system. This reduces enormously the amount of time required to clean up a major spill. This maneuver capitalizes on one of the little-known properties of liquid chlorine-its solubility in water. Under a slight pressure, such as the discharge from an eductor or pump, its solubility is 3 to 4 times that of chlorine vapor.

(4) Ton Container Flexible Connection Failure

Assuming a worst-case situation, the flexible connection breaks at the auxiliary container valve. Logic dictates that for a 120-psi cylinder pressure without the restriction of a header valve plus a 4 ft flexible connection, the release rate will exceed the rate from a header pipe rupture. A reasonable estimate would be a 20 percent increase: 11.4 x 0.2 = 13.68 1b/min.

(5) Fusible Plug Failure from Corrosion

A. Description

This is the most common problem of fusible plug failure. A 3/4-inch plug contains a lead core about 3/16 inch in diameter in a brass body. The inherent moisture in "dry" chlorine begins an immediate attack on the vulnerable brass body. Therefore, the hole generated by the corrosion is shaped like a cone with the base of the cone on the inside of the ton cylinder. The end result of this corrosive attack leads to a pinpoint hole between the brass body and the threaded steel of the dished cylinder head. Field observations indicate that this hole is never larger than 0.1 inch in diameter.

B. Liquid Release

For a worst-case situation the following calculations will be based upon a hole diameter of 0.15 inch, with the fusible plug located below the chlorine liquid level in the ton container. Here again the container pressure is assumed to be 120 psi.

Therefore:

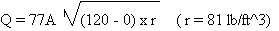
A = PI x D² / 4 = 3.1416 x (0.15)² / 4 =0.018 in²
A = 0.000125 ft²
Q = 77 x 0.00125 x (120 x 81)^1/2 lb/sec
Q = 77 x 0.00125 x 98.59 = 0.949 lb/sec
Q = 56.94 lb/min

C. Vapor Release

This is an important comparison because knowing the huge difference in the release rate, the safety crew should attempt to rotate the leaking plug to the vapor area. If this is done, the escaping vapor will cool the liquid to 40^oF in 3-4 minutes. This has to be taken into account when using the Chorine Institute formula:

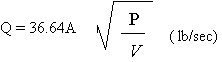
The container pressure will have been reduced enormously because the escaping vapor is at zero gage pressure. There is little doubt that the container pressure will be as low as 40 psi. Then V will be chosen for the density of chlorine vapor at 40 ^oF, which is 0.77 lb/ft.

Then:

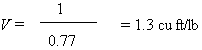
Therefore:

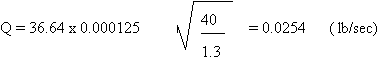
Q = 1.52 lb/min

D. Fusible Plug Blow-out

There is no such occurrence on record but it always remains a possibility. This is almost equivalent to a container rupture. It is assumed that the total discharge will be liquid chlorine. The container pressure will drop dramatically in the first few seconds, similar to a flash-off. For the sake of a rational calculation it will be assumed that the container pressure drops to 30 psi. This is equivalent to a liquid temperature of 20^oF; therefore, the density of the liquid chlorine is 93 1b/ft. So the leak rate is calculated as follows;

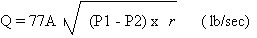
r = density at 20^oF = 93 lb/ft³
A = PI x D² / 4 = 3.1416 x (0.75)² / 4 = 0.44 in = 0.003 ft²

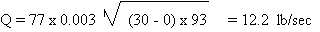
Q = 732.09 lb/min

It is quite obvious that the calculations indicate an impossibility. The contents of the container could never be discharged at that rate; otherwise the container would be empty in less than 3 minutes! The scenario that is closer to what will happen is a sudden cooling of the liquid chlorine that brings the container pressure to atmospheric, whereby the liquid chlorine will go into a freezing and thawing cycle that may take hours for the chlorine to escape.

4) Summary of Catastrophic Leak Events

• Whenever there is a major leak, the flash-off phenomenon will always prevent a positive pressure condition in a containment structure. The sudden vaporization due to flash-off cools the closed area so fast and so much that a negative pressure in the room is the result.
• There will always be a significant amount of liquid chlorine that must be dealt with as soon as possible. Because it much more soluble in water than chlorine vapor, it can be disposed of quite easily by a water-operated eductor or a liquid chlorine pump.
• The only way that liquid chlorine can be cooled by a leak is to withdraw vapor from it. Liquid flowing out of container due to a major leak will not cool the container or reduce the vapor pressure unless the leak is a large hole in the container such as a fusible plug blow-out. When this type of leak occurs, the flash-off phenomenon goes into action as soon as the liquid chlorine is exposed to the open room. This will always cool the room so quickly that it will produce a negative head in the room.

5) Calculating the Area Affected by Chlorine Releases

Whenever there is a major liquid chlorine spill, a vapor cloud is certain to form if the vapor is released to the atmosphere. This may not occur if the leak is from the gas phase of the system, because of the initial dilution of the vapor with air at its source. Chlorine vapor is readily amenable to following air currents, whether they be ventilation air or atmospheric air, largely owing to the available moisture in the atmosphere. The higher the humidity, the greater is the attraction of chlorine. The behavior is synonymous with the suck-back phenomenon.

A great many researchers have investigated the phenomenon of major releases of hazardous chemicals. The equation used by most investigators is the Gaussian Plume Model equation. This predicts the length and shape of the cloud formed from the initial release provided weather conditions are known. The cloud that emerges from this model is shaped like a cone sliced in half with the flat part at ground level and the apex at the source of the release. The value of the mathematical model is to assist authorities to set reasonable boundaries for evacuation after a release has occurred. The Gaussian equation takes into account release rate, the standard deviation of the crosswind plume, width and height of plume, height of initial source, and downwind, crosswind and vertical distances, and chlorine concentration as follows:

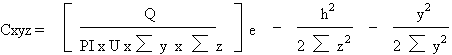
where:
C = concentration units/m
Q = release rate, units/sec
S_y, S_z = the standard deviation of the crosswind plume (width and height in meter)
U = mean wind speed velocity (m/sec) at h.
h = release source height (meters)
x, y, z = downwind, crosswind, and vertical distances (meters)

There are three factors not accounted for in the above plume model. These are: ambient temperature, relative humidity, and local terrain. These factors contributed significantly to the fatalities in the Youngstown accident. A release in a fog- shrouded area is probably the worst case. Air movement in a low-lying fog-shrouded area is usually nil. The relative humidity is at the saturation point, which allows the moisture-seeking chlorine gas to saturate the fog shroud. Clothing on the people in the release area will absorb the chlorine-laden moist air, thus multiplying the inhalation of chlorine. In such cases it is not sufficient to merely evacuate the area quickly. Exposed persons must remove their clothing as soon as possible. This adds another dimension of risk because a fog usually occurs in an area where the ambient temperature is quite low.

While fire is to be avoided at all costs where chlorine containers are stored, a brisk fire adjacent to a chlorine release can be a big help. This was demonstrated in a recent derailment when a tank car was ruptured by a following propane car, which exploded and caught on fire. The heat from the burning propane produced a chimney effect and the entire contents of the 90-ton tank car escaped without anyone suffering from chlorine inhalation.