| Prior
to selecting and ordering a specific type
and size of coupling, many related specifications
should be reviewed. In advance, you will
have to know how the length of shafts are
limited per the shaft models.
(1) Maximum DBSE: From above equation the
maximum DBSE could be simply calculated
as follows;
L2 = (K/ Critical Speed) x (OD2
+ ID2)0.5 (Critical
Speed = Safety Margin x Rated Motor Speed)
Example, motor rated speed = 1,800 rpm,
OD of selected shaft = 6.25 inch, ID of
selected shaft = 6.00 inch, K = 7,583,000.
Then, the DBSE at 1.40 and 1.35 safety factor
is obtained from above equation;
* Maximum DBSE = {(7,583,000/(1,800
x 1.4) x 6.252 + 62)1/2}0.5
= 161.5 inch at 1.40 of
service factor
* Maximum DBSE = {(7,583,000/(1,800
x 1.35) x 6.252 + 62)1/2}0.5
= 164.4 inch at 1.35 of
service factor
(2) Maximum Horse Power: The maximum horse
power at the given motor speed is obtained
from below equation.
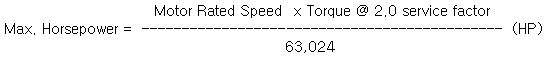
Where, Torque in Lb-in
63,024 = Unit Conversion Correction Coefficient
(3) Procedure of Selecting Optimum Models
A. Calculation of Basic Application Torque
(BAT): Calculate BAT first in accordance
with below formulas:
* English Unit BAT = (63,024
x HP of Motor) ?RPM of Motor (Lb-in)
* Metric Unit BAT = (974 x
KW of Motor) ?RPM of Motor (Lb-in)
B. Determine Design Torque: BAT x Service
Factor (Generally 2.0 in cooling tower)
C. Calculating of DBSE: DBSE of shaft =
12 x (Fan Diameter * 2) - (Distance between
of Center of Gear Reducer and End of High
Speed Shaft) + (Distance between Tip of
Fan Blade and End of Motor Shaft)
D. Selecting Models: Select the coupling
size equal to or greater torque which provides
a continuous torque at the given service
factor, and which satisfy the DBSE.
E. Checking Maximum Bore Sizes: After selecting
the coupling size, check the bores of gear
and motor shaft couplings. If the bore sizes
you specified are larger than the maximum
bore of selected coupling model, you have
to increase the coupling size to satisfy
your specified bores.
F. Checking Frequency Safety Margin with
BPF per previously described lateral critical
speed.
We are selecting the coupling shafts per
our own developed computer programs and
are usually providing the calculation data
sheet when to propose the shaft quotation.
Refer to the attached data sheet for your
reference. When you see it, you will have
to check the resonant frequency especially.
3) Sample Calculation
Let's look at a typical case of shaft selection
for the following design conditions.
- Fan Diameter: 30 feet
- Number of Fan Blade: 8 each
- Fan BHP: 144.1/41.7 HP
- Fan Speed: 126.4/84.3 RPM
- Motor HP: 175/60 HP
- Motor Speed: 1,770/1,180
RPM
- DBSE: 163.970 inch
- Service Factor: 2.0
- Used Gear Reducer: AGC-1712-14.0
First, determine the basic application torque
by taking the following steps and choose
the size satisfying the torque & DBSE
from the maker's data. Then, check for the
critical speed. If everything is OK, the
optimum model has been selected.
(1) Calculation of Basic Application Torque
& Design Torque
BAT = (63,024 x HP of Motor) ?RPM of Motor
(Lb-in)
= 63,024 x 175 ?1,770 = 6,231.2 Lb-in
Design Torque = BAT x Service Factor = 6,231.2
x 2.0 = 12,462.4 Lb-in
(2) Calculation of DBSE: If the DBSE is
not given by cooling tower designers, the
DBSE can be calculated.
DBSE = (Fan Diameter * 2) - (Distance between
of Center of Gear Reducer and End of High
Speed Shaft) + (Distance between Tip of
Fan Blade and End of Motor Shaft)
= 12 x (30?/ 2) - 33.750?+ 17.720?= 163.970?nbsp;
(3) Selecting Model: Model satisfying above
the design torque and DBSE is LMC 500.625.
After selecting the coupling size, check
the bores of gear and motor shaft couplings.
If the bore sizes you specified are larger
than the maximum bore of selected coupling
model, you have to increase the coupling
size to satisfy your specified bores. For
the size of bore exceeding the standard
size and not exceeding the maximum size,
additional cost shall be charged.
(4) Checking the Frequency Safety Margin:
First, the blade passing frequency must
be calculated per below, and the critical
speed must be calculated, and then must
be checked if 1 x BPF, 2 x BPF & 3 x
BPF is run within the range of + 5% to -
10% of critical speed.
BPF = (Number of Fan Blade x Fan Speed)
= 8 x 126.4 = 1,011.20 CPM
1 x BPF = 1 x BPF
= 1 x 1,011.20 = 1,011.20 CPM
2 x BPF = 2 x BPF
= 2 x 1,011.20 = 2,022.40 CPM
3 x BPF = 3 x BPF = 3 x 1,011.20 = 3,033.60
CPM
Critical Speed = (K / DBSE2)
x (OD2 + ID2)0.5
= (7,583,000 ?163.9702) x (6.252
+ 6.002)0.5 = 2,443.56
CPM
+ 5% Critical Speed = 1.05 x Critical Speed
= 1.05 x 2,443.56 = 2,565.74 CPM
- 10% Critical Speed = 0.9 x Critical Speed
= 0.9 x 2,443.56 = 2,199.20 CPM
Any blade passing frequencies are not within
the range of 2,199.20 to 2,565.74 CPM. Therefore,
this selection is fine to operate the shaft
at above design conditions. Finally, the
minimum resonant frequency margin can be
calculated as follows; blade passing frequency
which is most close to the critical speed
is 2 x BPF.
Resonant Frequency Margin = (Critical Speed
- 2 x BPF) / Critical Speed x 100 (%)
= (2,443.56 - 2,022.40) / 2,443.56 x 100
= 17.235 %
(5) Multi Speed Operation: If the motor
is controlled by two speed, the shaft selection
must be checked against the both speeds.
In general, the type of fan torque is variable
so that the motor must have the type of
variable torque. Accordingly, the selection
of shaft at the high speed satisfies the
continuous torque at the low speed. However,
the resonant frequency safety must be checked
if the blade passing frequency is not in
the range of critical speed.
BAT = (63,024 x HP of Motor) / RPM of Motor
(Lb-in)
= 63,024 x 60 ?1,180 = 2,304.6 Lb-in
Design Torque = BAT x Service Factor
= 3,204.6
x 2.0 = 6,409.2 Lb-in
LMC 500.625 selected is satisfying this
torque at the 1,200 RPM of motor speed and
the 163.970?of DBSE. The next to do is to
checking the resonant frequency safety margin.
BPF = (Number of Fan Blade x Fan Speed)
= 8 x 84.3 = 674.40 CPM
1 x BPF = 1 x BPF = 1 x 674.40 = 674.40
CPM
2 x BPF = 2 x BPF = 2 x 674.40 = 1,348.80
CPM
3 x BPF = 3 x BPF = 3 x 674.40 = 2,023.20
CPM
Critical Speed = (K / DBSE2)
x (OD2 + ID2)0.5
= (7,583,000 /
163.9702) x (6.252
+ 6.002)0.5
= 2,443.56 CPM
+ 5% Critical Speed = 1.05 x Critical Speed
= 1.05 x 2,443.56 = 2,565.74
CPM
- 10% Critical Speed = 0.9 x Critical Speed
= 0.9 x 2,443.56
= 2,199.20 CPM
Any blade passing frequencies are not within
the range of 2,199.20 to 2,565.74 CPM. Therefore,
also this selection does not matter to operate
the shaft at above design conditions. Finally,
the minimum resonant frequency margin can
be calculated as follows; blade passing
frequency which is most close to the critical
speed is 3 x BPF.
Resonant Frequency Margin = (Critical Speed
- 3 x BPF) / Critical Speed x 100 (%)
= (2,443.56 - 2,023.20) ?2,443.56
x 100 = 17.203 %
|